写在前面

​ 在我们所熟知的基本数据类型中，**long ** 超长整型是表达最大整数的数据类型，但是当我们处理的数字结果超过这个类型的数据范围时，就会造成数据溢出而导致结果无法正常显示。这时候我们就可以用字符串来代替处理超长整数的运算，以下则是用C语言实现超长整数的四则运算。

大数加法

刚才已经说到，大数运算的思路应该首先是将数字以字符的形式存储在字符串数组中。在利用数字字符对应的ASCII码表值进行运算、

思路解析

  • 将输入的字符进行处理不接受除了‘0’-‘9’以外的字符
    • 此处用到的getch()函数，其作用是从控制台取得一个字符，无回显
  • 根据小学加法的运算规则，我们知道数字相加首先要右对齐，接着上下对应位置的单个数字从右向左依次进行相加，如果和数大于10则要给右面进行相加的数字进1,而自身则是减10；根据此规则我们可以定义AddChar(char ch1,char ch2)函数计算两个数字字符的结果，并且要给全局变量Tag赋值为进位1。
    • 如：’2’+’4’=’6’，tag=0 ; ‘6’+’7’=’3’，tag=1
  • 之后我们就可以进行两个数字字符串的算法，定义AddNumberStr(char a[],char b[],char c[])函数，在c[]字符串中存储相应的两数之和。注意一定要些字符串的结束标志’\0’

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
//超长整数的加法
#include<stdio.h>
#include<conio.h>
#include<string.h>
#define N 20

void beep();
void GetNumberStr(char s[]);
void AddNumberStr (char a[],char b[],char c[]);
char AddChar (char ch1,char ch2);
void LeftTrim(char str[]);

int tag=0;

void beep(){
    printf("\07");
}

void GetNumberStr(char s[]){
    int i = 0;
    char ch;
    while (1)
    {
        ch=getch();
        if (ch=='\r')
            break;
        
        if (ch=='\b')
        {
            if (i>0)
            {
                printf("%c %c",ch,ch);
                i--;
            }
            else{
                beep();
            }
            continue;
        }
        if (ch<'0'||ch>'9')
        {
            beep();
            continue;
        }
        if (i<N)
        {
            printf("%c",ch);
            s[i++]=ch;
        }
        else{
            beep();
        }
    }
    s[i]='\0'; 
}

char AddChar (char ch1,char ch2){
    char ch;
    ch = (ch1-0x30+ch2-0x30)+tag;
    if (ch>=10)
    {
        tag=1;
        return (ch-10+0x30);
    }
    else{
        tag=0;
        return (ch+0x30);
    }
    
}

void AddNumberStr(char a[],char b[], char c[]){
    int i,j,k;
    memset(c,' ',N+2);
    i=strlen(a)-1;
    j=strlen(b)-1;
    k=N;
    while (i>=0&&j>=0)
    {
        c[k--]=AddChar(a[i--],b[j--]);
    }
    while (i>=0)
    {
        c[k--]=AddChar(a[i--],'0');
    }
    while (j>=0)
    {
        c[k--]=AddChar(b[j--],'0');
    }
    if (tag==1)
    {
        c[k]='1';
    }
    c[N+1]='\0';
    LeftTrim(c);
}

void LeftTrim(char str[]){
    int i;
    for ( i = 0; str[i]==' '; i++)
    {

    }
    strcpy(str,str+i);
}

void main(){
    char a[N+1]={0},b[N+1]={0},c[N+2];

    printf("a=");
    while (strlen(a) == 0)
    {
        GetNumberStr(a);
    }
    printf("\nb=");
    while (strlen(b) == 0)
    {
        GetNumberStr(b);
    }
    
    AddNumberStr(a,b,c);
    printf("\n a+b=%s \n",c);
}

大数减法

思路解析

  • 和加法相同的是，减法运算也应该是将两串数字右对齐(即从最高位开始计算)。
  • 定义DeleteChar(char ch1,char ch2)函数对两个数字字符进行相差运算，需要注意的是两个数字字符相差就是要的数字，不需要减去‘0’。
  • 定义DeleteNumberStr(char a[],char b[],char c[])函数，同加法一样，进行一位一位 的减。

代码

为了代码简介并且更加明了，只贴了和大数加法不同的地方。另外的部分与加法不同的细节需要大家自行更改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
char DeleteChar(char ch1,char ch2){
    char ch;
    ch = (ch1-ch2)-tag;
    if (ch<0)
    {
        tag=1;
        return (ch+0x30+10);
    }else{
        tag=0;
        return (ch+0x30);
    }

}

void DeleteNumberStr(char a[],char b[],char c[]){
    int i,j,k;
    memset(c,' ',N+2);
    i=strlen(a)-1;
    j=strlen(b)-1;
    k=N;

    while (i>=0&&j>=0)
    {
        c[k--] = DeleteChar(a[i--],b[j--]);
    }
    while (i>=0)
    {
        c[k--] = DeleteChar(a[i--],'0');
    }

    if (tag == 1)
    {
        c[k] = a[i] - b[j] - 1;
    }
    c[N+1] = '\0';
    LeftTrim(c);
}

大数乘法

思路解析

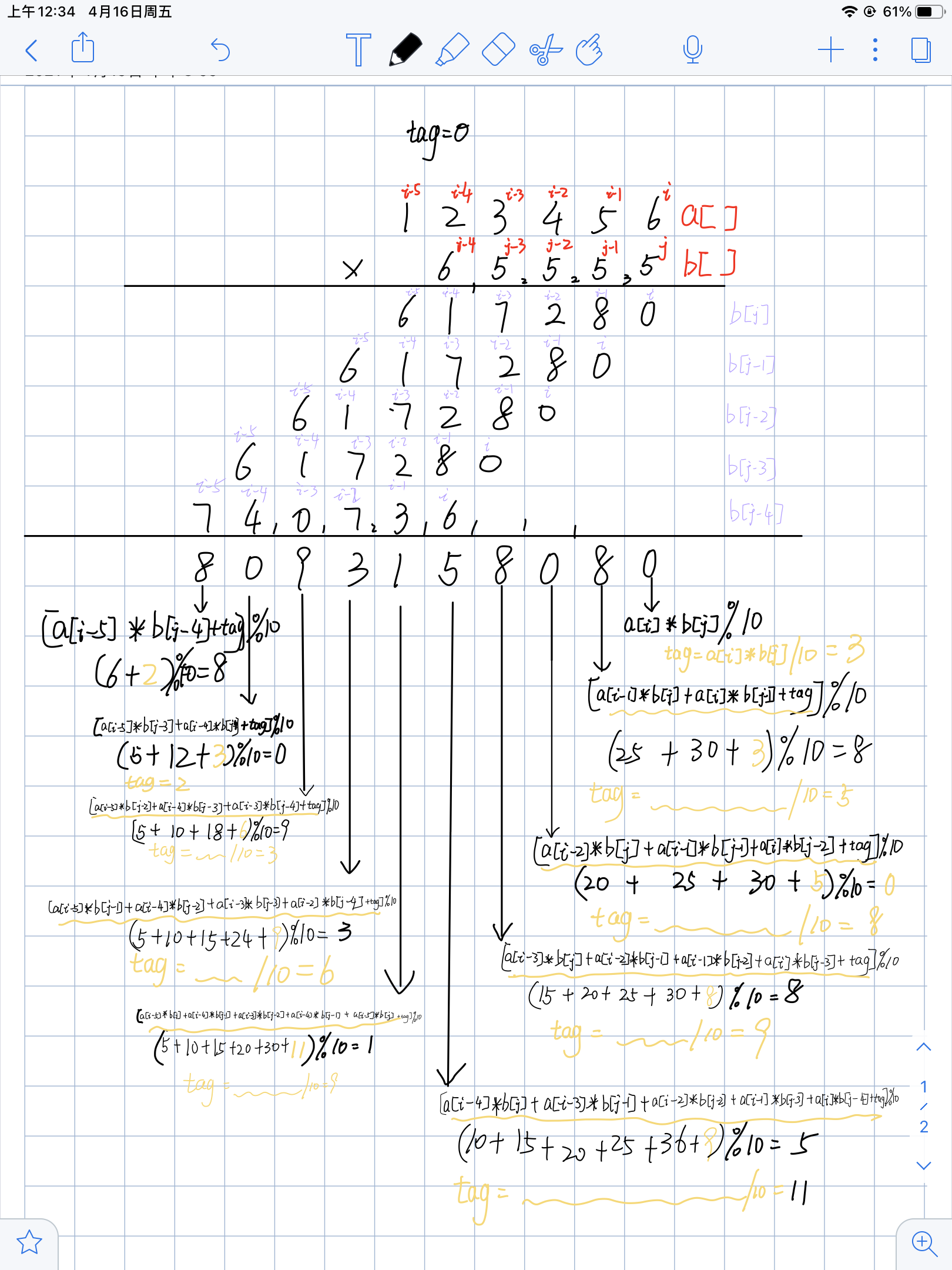
  • 乘法与加减法的思路有所不同，但是我们知道，我们必须保证是一位一位的运算。根据下面的图片分析之后可以知道。结果中的每一位数字都可以由两个数字字符串中各取一个数字相乘以后求和在取余得到 。而所选取的所有项中都有一个规律，它们每项中a[]，b[]对应的下标之和是相同的。而进位则是该和数的商的整数部分。
  • 定义MultiplyNumberStr(char a[],char b[],char c[])函数，

大数乘法.PNG

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void MultiplyNumberStr(char a[],char b[],char c[]){
    int i,j,m,n;
    i=strlen(a)-1;
    j=strlen(b)-1;
    
    for(m=0; m< i+1; m++){
    	for(n=0; n< j+1; n++){
			c[m+n] += (a[m]-0x30)*(b[n]-0x30);
		}
	}
	
    for(m = i + j; m > 0; --m) {
        if(c[m] > 9) {
            c[m - 1] += c[m] / 10;
            c[m] = c[m] % 10 + 0x30;
        }else{
			c[m] += 0x30;  
		} 
    }
    
    c[2*N] = '\0';
}

大数除法

思路解析

  • 除法在运算过程中我们可以想到的是用被除数一直减去除数，减法进行的次数即为所得的商的整数部分。此方法简单但是有一个致命的弱点。当你的被除数远大于除数的时候 ，减法的次数操作过多就会造成计算及耗时过长，所以我们不采用对方法。
  • 考虑到除法的运算是从左往右的。并且有了前面加减乘算法中对结果一位一位的求解的启发。我们可以先将除数的长度变成与被除数并且末尾补‘0’，再用被除数一直去减去这个经过处理的除数，当结果小于被除数的时候，减法运算的次数即为商的第一位。之后，我们再将除数右移动一个位置(即末尾去除一个0)，继续进行减法运算。来确定商的第二位，其余位置同理。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
//超长整数的除法 
#include<stdio.h>
#include<stdlib.h> 
#include<conio.h>
#include<string.h>
#define N 20

void beep();
void GetNumberStr(char s[]);
void DivideNumberStr(char a[],char b[],int c[]);
void DeleteNumber(int m);
void LeftTrim(char str[]);
 
char a[N],b[N];
int c[N];
 
void main(){

    printf("a=");
    while (strlen(a) == 0)
    {
        GetNumberStr(a);
    }
    printf("\nb=");
    while (strlen(b) == 0)
    {
        GetNumberStr(b);
    }

    DivideNumberStr(a,b,c);

}

void GetNumberStr(char s[]){
    int i = 0;
    char ch; 
    while (1)
    {
        ch=getch();
        if (ch == '\r')
            break;
        
        if (ch == '\b')
        {
            if (i>0)
            {
                printf("%c %c",ch,ch);
                i--;
            }
            else{
                beep();
            }
            continue;
        }
        if (ch<'0'||ch>'9')
        {
            beep();
            continue;
        }
        if (i<N)
        {
            printf("%c",ch);
            s[i++]=ch;
        }
        else{
            beep();
        }
    }
    s[i]='\0'; 
}

void beep(){
    printf("\07");
}

void DivideNumberStr(char a[],char b[],int c[]){
    int i,j,k,m,n;
	memset(c,'0',N);
    n=strlen(a);
    m=strlen(b);
    
    k=0;
    while(1)
	    {
            c[k]=0;
            while(strcmp(a,b)>=0)
            {
                DeleteNumber(m);
                c[k]++;
            }
            k++;
            if(n==m)   break;
            for(i=m-1; i>=0; i--)
                b[i+1]=b[i];
            b[0]='0';
            m++;
            b[m]='\0';
        }
    printf("\n a/b=");
    i=0;
    while(c[i]==0) i++;
        for(; i<k; i++)
            printf("%d",c[i]);
    
    c[N+1] = '\0';
}

void DeleteNumber(int m){
    int i=0,j;
    while(1)
    {
        if(a[i]=='0') i++;
        else
        {
            j=i;
            break;
        }
    }
    for(; i<m; i++)
        a[i]=a[i]-b[i]+'0';
    for(i=m-1; i>j; i--)
        if(a[i]<'0')
        {
            a[i]+=10;
            a[i-1]--;
        }
}